提出了一种预应力多孔弹性复合材料的控制方程。我们研究的结构具有多孔弹性基质,其中嵌入弹性子相,孔隙中流动着不可压缩的牛顿流体。假定基体和各个子相均为线弹性和预应力。我们能够通过利用存在于孔隙尺度和材料总体尺寸(宏观尺度)之间的长度尺度分离来应用渐近均质化技术。我们推导了一种新的宏观尺度模型,该模型描述了弹性相具有预应力的多孔弹性复合材料。我们扩展了目前的文献为孔隙弹性复合材料解决预应力的作用,在新的系统的导数微分方程及其系数的函数形式。后者是通过求解适当的周期单元微分问题来计算的,该问题编码了与预应力有关的具体贡献。第一种情况下的模型是在最一般的情况下推导出来的,然后为与材料的不同宏观行为有关的各种特殊情况指定。
含有多孔弹性基体的材料,其流体在孔隙空间中流动,可以描述为多孔弹性材料,并使用孔隙弹性理论进行建模。这是Biot在进行了各种实验后在[1,2,3,4]中首次提出的。只有当存在一个尺度时,弹性矩阵和流体之间发生的相互作用以及发生在矩阵和流体中的相互作用才能被解决,该理论才能被应用。这是一个广泛应用的建模框架,有许多现实世界的问题。这些问题包括但不限于硬分层组织(发生小变形),如骨骼和肌腱[5,6]或健康和肿瘤生物组织中的间质基质[7]。它也适用于心脏(心肌),如[8,9]或动脉壁(参见例[10,11,12,13])。孔隙弹性理论不仅在人类生物学中有应用,它也被用于模拟人工结构和生物材料[14,15,16],并且在Biot的原始理论中,它可以应用于土壤和岩石力学[17,18]。

我们正在考虑以各种结构特征为特征的材料,这些结构特征通常在多个微观结构水平(尺度)上发现。由于我们是在模拟多孔介质,所以考虑一个不同固相和在孔隙中流动的流体之间发生相互作用的尺度是合适的。这个尺度被称为孔隙尺度。孔尺度是一个精细的微观结构水平,其相关长度远小于整个区域。整个物质可以用一个尺度来描述,我们称之为宏观尺度。
由于我们有一种包含多个尺度的材料,我们希望找到一种既能详细描述材料有效特性又能在计算上可行的模型。为了做到这一点,我们的目标是将宏观尺度的控制方程与孔隙尺度上发生的性质和相互作用联系起来。该过程的第一步是为孔尺度上发生的相互作用创建一个流固相互作用(FSI)问题。然后,这个问题可以用于上尺度过程,以获得宏观控制方程。升级过程可以通过文献中提出的各种技术来实现。这些方法可以被描述为均质化技术。这些均质化技术可以是以下的一些,包括混合物理论,有效介质理论,体积平均和渐近均质化。每种技术都有各种不同之处,应该根据预期的应用程序和希望编码的信息类型或从产生的宏观模型中获得的信息类型进行选择。有关这些技术的回顾和讨论,请参见[19,20]。
在本文中,我们采用渐近均匀化技术。该技术广泛应用于孔隙弹性领域,并在[18,21,22,23]中被用于推导Biot方程。孔隙弹性理论已经扩展到更复杂的动力学,例如包括溶质的生长、重塑和输运,参见,例如,通过使用渐近均质化技术[24,25]。该理论的发展还包括孔隙弹性材料的血管化[26]。近年来,该技术也被用于考虑弹性复合材料,如In[27]和微观结构更复杂的孔弹性材料,如孔弹性复合材料[28]和双孔弹性材料[29]。在[30]中也考虑了非局部扩散如何影响复合材料中化学物质的输运。尽管它的主要用途是在线性环境中作为对该技术的批评,但它最近也被用于经历大变形的孔弹性材料,如活性孔弹性材料[25]和非线性孔弹性复合材料[31]。通过渐近均匀化得到的模型在计算上也是可行的。文献[32]中考虑了孔隙率和微尺度固体基质压缩性对孔隙弹性材料力学行为的影响。然后在[33]中进一步发展以考虑宏观尺度行为。最近,研究人员在[34]中对多孔弹性复合材料的有效刚度进行了微观力学分析,其结果随后被进一步专门用于研究心肌梗死的结构变化[35],从而向在心肌梗死研究中使用分段线性弹性渐近均质化模型迈出了第一步。
我们将渐近均质化技术应用于流固相互作用(FSI)问题,我们建立了该问题来描述具有不可压缩牛顿流体在孔隙中流动的预应力多孔弹性矩阵和子相的行为。这种设置意味着弹性矩阵和各个子相都与流体流动接触。这种类型的结构适用于许多物理场景,特别是生物组织。例如,动脉壁模型可以考虑这种设置。在[36,37]中,作者提出了在预应力管中模拟动脉壁的FSI问题。我们所研究的结构可以适用于这种情况,因为我们可以识别基质部分与细胞外基质,弹性亚相与动脉壁微观结构中嵌入的胶原蛋白和弹性纤维[38]。在研究受有限应变影响的厚、不可压缩、各向同性弹性体的非线性稳定性分析时,也考虑了预应力[39]。
我们在一个尺度上考虑材料的成分,在这个尺度上,各种固体亚相和孔隙是清晰可见的,与基体不同。我们称这种规模为微观规模。这个尺度比整个材料要小得多(在整个材料中,孔隙或亚相不再明显可见),因此,我们称之为宏观尺度。然后,我们应用渐近均质化技术来升级FSI问题,考虑流体-固体和固体-固体界面上的牵引力、位移和速度的连续性,即在基质和流体之间、子相和流体之间、基质和子相之间。在准静态情况下,对于一般预应力,提出的新型宏观尺度模型为Biot型,是对孔弹性复合材料[28]的扩展。我们的模型包含额外的条款,以说明每个弹性阶段的不同预应力。我们能够通过假设基体和子相没有预应力来恢复[28]。模型的系数编码了微观结构的性质。这些是通过解决由于应用渐近均匀化技术而产生的微尺度微分问题来计算的。这些单元问题属于孔弹性复合材料的[28]类型,再加上其他问题,以解释所有弹性相之间的预应力差异。
我们能够将我们的模型的形式与[40]在没有流体相的情况下对电致伸缩复合材料的形式进行比较。[40]中的模型研究了渐近均匀化技术在线性弹性复合材料中的应用,该复合材料的变形是由广义Maxwell应力张量的散度驱动的。
本文的组织结构如下。我们首先介绍流固相互作用问题,该问题描述了我们在第2节中要考虑的材料域。该问题描述了预应力多孔弹性基质与子相之间的相互作用,以及在孔隙中流动的流体。在第3节中,我们对第2节中给出的FSI问题进行多尺度分析。通过这样做,我们得出了新的宏观尺度模型,描述了预应力多孔弹性复合材料的均匀力学行为。在第4节中,我们提出了新的宏观尺度模型,并讨论了预应力的各种选择。我们还提出了一种解决宏观尺度模型的方案,并将这里得到的结果与[40]在没有流体室的情况下得到的结果进行了比较。在第5节中,我们提供了我们工作的结论以及进一步的观点。我们还有附录。A,它包含了在此以分量符号表示的所有单元问题,这将有助于进行数值模拟。
我们首先考虑一个集合,其中代表固体多孔基质,连接的流体室和N个不连接的子相集合(可以代表包裹体或纤维)的结合,这样
(1)和。三维域的截面示意图如图1所示。
在描述控制我们结构中每个域的方程之前,我们首先希望澄清将在整个手稿中使用的符号。
(表示法)对于一个泛型域,我们使用下面的符号,对于标量,我们使用普通的小写字母,例如f,对于向量,我们使用黑体字,例如,然后,用于二阶张量。我们用在三阶张量上,最后用在四阶张量上。我们定义了将在这些量之间发生的操作,例如附录中四阶张量与二阶张量的双缩。A.在最终的宏观尺度模型中有一些例外,为了保持与用于比奥模量和比奥系数张量以及孔隙率的经典符号的风格一致。在这种情况下,Biot的模量为,Biot的张量为,孔隙度为[21,41]。
在不考虑体积力和惯性的情况下,得到固体区域的平衡方程为
(2)和
(3)关系(2-3)中出现的符号和分别表示对应于每个子相的固体柯西应力张量和对应于矩阵的固体柯西应力张量。然后我们假设基体和每个子相都是一般的线弹性固体,并且由于我们承认存在预应力,我们表示和为
(4a) (4b)式中,和分别为各子相和基体中的弹性位移,和分别为子相和基体中的预应力。(4a)和(4b)中的第一项是柯西应力的本构表达式。
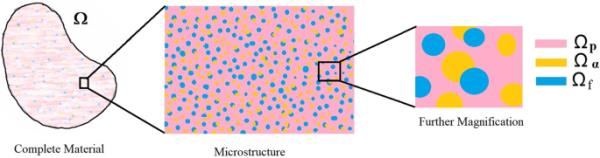
二维草图显示三维领域和两种不同的放大水平。在最放大的(微尺度)中,流体相用蓝色表示,多孔基质用粉色表示,亚相用橙色表示。包裹体和/或纤维可以潜在地与基质和在孔隙中流动的流体接触,或者它们可以完全嵌入基质中。请注意,表示流体和包裹体/纤维的点的大小不同,并不意味着这两个阶段彼此相交。相反,它仅仅意味着子相和流体通道具有各种几何形状和弹性特性
四阶张量和分别是各子相和矩阵中的弹性张量,分别具有对应的分量和。我们注意到,每个和都配备了右小调和大调对称,即
(5a) (5b)因此,也留下了小的对称接着是(5a-5b)特别地,通过应用右次对称,我们可以等价地将方程(4a-4b)改写为
(6a) (6b)在哪里
(7)是梯度算子的对称部分。
液体舱的平衡方程是这样的
(8)其中为流体应力张量。我们假设流体室是不可压缩的牛顿流体,所以的本构方程由
(9)式中为流体速度,p为压力和粘度,以及不可压缩性约束
(10)将式(9)代入式(8)并使用无散度条件(10)得到Stokes问题
(11)为了解决整个领域的流固相互作用问题,我们还需要流体和固相之间的界面条件。我们首先将流体相与包裹体/纤维之间的界面定义为
(12)矩阵和流体之间的是
(13)然后我们在每个和上施加速度和应力的连续性,即
(14a) (14b) (14c) (14d)式中,分别为各子相和基体的固相速度。与界面垂直的单位向外(即指向流体域)矢量分别用和表示。
最后,我们需要在每个固体子相和基体之间的界面上应力和位移的连续性。我们定义这个边界为
(15a) (15b),其中为指向内含物的接口的法向单位向量。
在下一节中,我们将进行多尺度分析。这涉及(i)我们在本节中描述的偏微分方程(PDEs)(2)、(3)、(8)和(10)以及界面条件(14a) - (15b)的无量纲化,(ii)引入两个分离良好的长度尺度,(iii)将渐近均质化技术应用于所得到的偏微分方程的无量纲系统,以及(iv)推导整个材料的有效控制方程。
我们现在对上一节介绍的流固相互作用问题进行多尺度分析,总结如下
16 (16) (b) (16) (16 d) (16 e) (16) (16 g) (16 h) (16) (16 j)其中,利用应力关系(6a)、(6b)、(9),结合不可压缩性约束(16d),平衡方程(16a)、(16b)、(16c)也可以改写为
(17a) (17b) (17c)。然后,通过规定合适的外部边界条件来关闭问题(16a-16j)。
我们的系统本质上是多尺度的。特别地,我们用L(宏观尺度)表示整个区域的平均尺寸,而d表示孔隙尺度(微观尺度),这里假设它与与基质相互作用的相邻子相与流体区域之间的距离相当。为了强调这些尺度之间的差异,对pde (16a-16j)系统进行无量纲分析是有帮助的。我们进行无量纲分析,假设系统的特征是参考压力梯度C,特征(参考)流体速度由典型的抛物线轮廓给出,与牛顿流体在半径d的圆柱体中缓慢流动成正比。
因此,在我们的例子中
(18)然后我们利用(18)并观察它
(19)得到pde (16a-16j)体系的无量纲形式,即
(20) (20 b) (20 c) (20 d) (20 e) (20) (20 g) (20 h)(20我)(20 j),这里为了简化符号,我们去掉了。应力张量(6a)、(6b)和(9)的无量纲对应项由式给出
(21a) (21b) (21c)这样平衡方程(20a-20c)就改写了
(22a) (22b) (22c)在哪里
(23)在下一节中,我们将介绍渐近均质化技术,该技术通过正式假设微观尺度和宏观尺度分离良好,用于提高PDEs (20a-20j)的无量纲系统。
在本节中,我们介绍了用于推导方程(20a - 20j)的宏观尺度模型的双尺度渐近均匀化技术。我们首先假设微尺度的特征长度,用d表示,代表孔隙和单个包裹体/纤维被清楚分解的长度尺度,与区域L的平均尺寸相比是小的,即。
(24)然后,我们引入一个局部空间变量,通过设置来捕捉场的微观变化
(25)空间变量和被认为是形式上独立的,分别代表宏观尺度和微观尺度。然后,梯度算子变换为
(26)梯度算子的对称部分变换为
(27)我们进一步假设所有的场,以及弹性张量和,都是和的函数。我们还假设域,和可以用幂级数展开来表示,即。
(28)其中统称为本分析中涉及的每个领域。
为了进行微观结构分析,我们希望将重点放在单个周期电池上。为了做到这一点,我们假设我们目前分析中的每个场都是-周期的。这一假设允许由渐近均匀化技术引起的微尺度微分问题在域的有限子集(周期单元)上得到解决。
然而,所有字段都是周期性的这一假设对于继续分析来说是不必要的。相反,我们可以只假设场的局部有界性。这种方法意味着我们只能确定宏观尺度模型的功能形式。假设局部有界得到的系数与要在材料整体微观结构上解决的微观问题有关。这实际上是不可能的,如果不是令人望而却步的计算。在[21,42]中找到了一些局部有界假设的例子。
(宏观均匀性)给定材料的微观几何形状可以随宏观尺度上的单个点而变化。下文[21,24,43,44,45]考虑了微观结构的这种变化,并通过适当应用雷诺输运定理在最终宏观尺度模型中出现附加项。为了简化模型的推导,通常忽略微观结构对宏观尺度点的依赖。也就是说,我们假设在每一个宏观尺度的点上,微观尺度都是相同的。这就相当于说微观几何不依赖于。我们称这种性质为宏观均匀性。我们在这里做了这个假设。因此,对于积分号下的微分,我们得到如下结果
(29)其中是张量或矢量。
(孔隙尺度几何)为了清晰地呈现,并且不损失模型属性的一般性,我们可以通过假设每个周期单元中只包含一个子相位来限制我们的分析,如图2所示。如果有必要,该模型可以很容易地扩展到周期单元内的许多子阶段。因此,索引不再需要,我们相应地调整了符号。我们用相应的周期细胞识别域,纤维/包涵体、基质和流体细胞部分分别用和表示。不同相位之间的界面用和表示,用相应的单位法向量和表示。
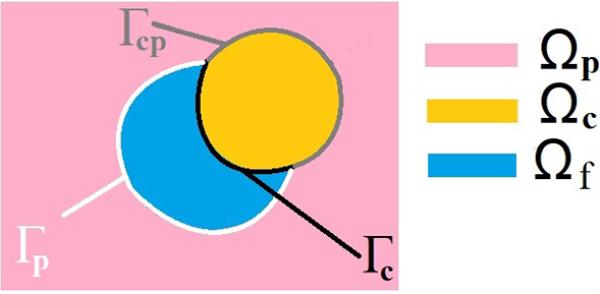
我们所关注的周期细胞的二维截面示意图。我们有一个用橙色表示的亚相/纤维,它与粉红色表示的基质和蓝色表示的液体接触。我们还强调了各个阶段之间的接口
我们将渐近均匀化假设(26)和(28)应用于方程(20a-22c),考虑到周期性,得到以下偏微分方程的多尺度系统
30 (30) (b) (30 c) (30 d) (30 e) (30) (30 g)(30小时)(我)30 (30 j)具有由。给出的,,,的多尺度表达式
(31a) (31b) (31c)而平衡方程以,,,,读
(32a) (32b) (32c)现在我们可以将(28)型幂级数代入(30a?32c)中的相关字段。然后,通过求解的系数,我们导出了材料在相关的前导(零)阶场中的宏观尺度模型。当渐近展开式中的一个分量保持对微观尺度的依赖时,我们可以取积分平均值,我们将其定义为
(33)由于-周期性,积分平均可以在一个代表性单元上进行,并且是域的体积,积分在微观尺度上进行。我们注意到这一点。由于假设为-周期性,可以对一个有代表性的单元格进行积分平均。因此,(33)表示细胞平均值。为了简洁起见,我们还引入了符号
(34)对于具有限制的字段,并分别在实体单元格部分或中定义。
将in (30a - 30j)的系数相等,得到
(35) (35 b) (35 c) (35 d) (35 e) (35) (35 g)(35小时)(35我)(35 j),的应力方程(31a?31c)的系数为
(36a) (36b) (36c)而平衡方程(32a?32c)的系数为
(37a) (37b) (37c)同样,我们现在希望将方程(30a-30j)中的系数相等,它给出
(38) (38 b) (38 c) (38 d) (38 e) (38) (38 g) (38 h)(38我)(38 j),的应力方程(31a?31c)的系数为
(39a) (39b) (39c)而平衡方程(32a?32c)的系数为
(40a) (40b) (40c)我们现在可以从(35c)和(36a)中看到,它不依赖于微观尺度变量。也就是说,
(41)从(36b)和(36c)以及周期性条件中,我们也得到了这一点,并且与微观尺度变量无关,尽管它们通常仍然依赖于宏观尺度变量和时间t,参见[21,23]。也就是说,
(42a) (42b)既然有了边界条件,我们就可以定义
(43)我们将在接下来的部分中使用它。
现在我们要研究一下我们所表示的速度的阶数。我们可以用。来定义相对流固位移
(44)利用式(36a)、(35e)、(35f)、(38c)和(39a),利用符号(43),我们得到一个Stokes型边值问题,它由式给出
(45a) (45b) (45c)现在利用线性并使用式(41),我们可以对stokes型边值问题(45a-45c)提出如下解析:
(46) (47)其中定义为任意常数函数。式(47)是在二阶张量和向量满足以下单元问题的情况下(45a?45c)问题的解
(48)在边界上适用周期性条件,并且要为解的唯一性设置进一步的条件(例如,流体单元部分的平均值为零)。在流体域中取(46)的积分平均值,得到
(49)这意味着流体的流动在宏观尺度上是由达西定律描述的。
我们现在需要弹性位移和。求和方程的积分平均值。(38a) (38b)和(38c)我们有
(50)将散度定理应用于前三个积分,并利用宏观均匀性对后三个积分进行重排,得到
(51)其中,,,,和分别为,,,,和对应的单位法线。由于外边界上的贡献,由于-周期性而抵消,式(51)变为
(52)(52)中的前六个积分由于(38g) (38h)和(38i)消去了,最后三项可以写成
(53)其中为材料的孔隙率。
利用式(41)和式(43),利用式(35a)、式(35b)、式(35g)、式(35h)、式(35i)、式(36a)、式(38j)、式(39b)和式(39c),我们可以写出和的以下问题
(54a) (54b) (54c) (54d) (54e) (54f)利用线性,(54a?54f)给出的问题的解为
(55) (56)其中和是三阶张量,和是向量。辅助字段,,,,并解决以下单元格问题
(57a) (57b) (57c) (57d) (57e) (57f)和
(58a) (58b) (58c) (58d) (58e) (58f)和
(59a) (59b) (59c) (59d) (59e) (59f)现在我们考虑一级固体应力张量。因为从(39b)和(39c)我们得到了和分别与和相关,我们可以写
(60)和
(61)我们在这里定义
(62)将(60)和(61)相加,在固体域上求积分平均值,得到
(63)从(53)中,我们得到了这个
(64)在哪里
(65)我们可以将式(64)和式(65)描述为孔弹性复合材料的平均力平衡方程。
我们现在回到(38d),不可压缩条件并积分得到
(66)将散度定理两次应用于第一个积分,利用(38e)和(38f)并重新排列第二个积分,我们得到
(67) (68)因此,我们有
(69)用式(55)和式(56)和式(62),就得到了这个
(70)用式(70),式(69)变成
(71)现在回到(44),相对流固位移的表达式,并在流体域上取积分平均值,我们得到
(72)其中为材料的孔隙率。然后用的平均值重新排列,我们得到
(73)然后我们将使用这个关系重写(71)为
(74)我们可以展开(74)的左边,然后重新排列得到下面的表达式。我们注意到我们可以表示为。然后
(75)然后我们可以定义
(76)然后,我们可以把(76)写成(75
(77)最后除以,得到
(78)我们现在已经推导出了所有的方程,可以用来描述多孔弹性复合材料的宏观模型。
宏观尺度模型中的方程描述了材料在准静态状态下的孔隙压力、平均流体速度和弹性位移的有效孔隙弹性行为。宏观尺度模型由
(79a) (79b) (79c) (79d)这是宏观压强,是一级固体位移,是一级固体速度。该新模型包括控制流体流动的方程(79a)。该方程符合达西定律,不受预应力弹性相的影响。我们知道(79b)是材料的平衡方程,本构律由(79c)给出。本构律结合了预应力的影响,包括在每个阶段和附加项中的领先级预应力,以及解决单元问题(59a) - (59f)所产生的影响,这些问题解释了微观结构不同点的预应力差异。最后一个方程(79d)是质量守恒方程,它是孔弹性复合材料的守恒方程,但增加了一项,它解释了微观结构中不同点的预应力差异。
宏观尺度模型的推导没有详细说明每个弹性阶段的预应力。现在我们将考虑以下情况,并详细讨论每种情况对宏观尺度模型和用于计算模型系数的单元问题的影响。
对两个尺度的依赖性
在预应力和依赖于微观尺度和宏观尺度的情况下,我们精确地导出了宏观尺度模型(79a) - (79d)。流体的细胞问题不涉及预应力,因此仍为(48)。在单元的固体部分的情况下,我们有问题(57a) - (57f)和(58a) - (58f)不受预应力的影响;但是,(59a) - (59f)会受到影响。我们可以看到(59a) - (59f)我们有预应力。如果我们假设这些张量同时依赖于微观尺度和宏观尺度,那么孔尺度周期细胞问题就依赖于宏观尺度,因此不容易解决。这些依赖于两个尺度的预应力意味着两个尺度没有完全解耦,因此,这极大地增加了计算复杂性。当然,也有新兴的技术可以用来尝试解决数值耦合问题[46]。该技术涉及使用人工神经网络(ann)快速,准确地升级和定位问题。这是通过增量数值方法进行的,其中存在与当前变形或应力相关的细胞属性的重排,这意味着在每个增量时间步之后都有宏观模型的重塑。该方法适用于有限应变和大变形问题,而在每一个增量时间步内只会有无穷小的变形或应力变化。如果材料是包含预应力(无孔隙)的弹性复合材料,则可以使用类似于[47]中概述的分层层状弹性材料的方法,其材料性能仅沿一个方向变化。然而,由于孔隙的存在,这种方法不能用于该模型。在生物组织中,如动脉壁或心肌中[36,37,38],最可能出现的情况是,预应力的微尺度胶原蛋白和弹性纤维导致材料的宏观残余应力。
预应力分解为两个组合在一个尺度上有变化的事物
我们可以潜在地解决两个尺度耦合的另一种方法是,建议将预应力分解为两部分,一部分取决于宏观尺度,另一部分仅取决于微观尺度。我们做了以下假设:首先,弹性张量只依赖于微观尺度
(80)其次,对超前预应力进行如下分解
(81a) (81b)其中新的上标L和G分别代表局部(微观)和全局(宏观)。在这里,我们以这样一种方式进行了分解,即第二级预应力是由第四级微观分量与第二级宏观分量的双重收缩产生的。我们需要在我们提出的弹性问题(54a) - (54f)的分析中考虑这种分解。我们提出的新解决方案为
(82a) (82b)其中,,,,和是只依赖于微尺度变量的三阶张量,和是依赖于微尺度变量的向量。现在有两种选择可以导致不同的细胞问题。如果我们假设二阶张量,那么我们得到以下不保留任何宏尺度依赖性的单元问题
(83a) (83b) (83c) (83d) (83e) (83f)和
(84a) (84b) (84c) (84d) (84e) (84f)这是细胞问题(57a) - (57f)和(58a) - (58f)现在是依赖的,因为我们做了假设(80)。我们有细胞问题的变化包括我们分解的预应力,这些是
(85a) (85b) (85c) (85d) (85e) (85f)和
(86a) (86b) (86c) (86d) (86e) (86f)这些细胞问题可以在微观尺度上完全解决。
如果我们假设二阶张量
(87)然后我们可以把(82a) - (82b)写成
(88a) (88b)和是只依赖于微尺度变量的三阶张量和是只依赖于微尺度的向量。这允许我们获得以下不保留任何宏尺度依赖性的单元问题。我们正好有(83a) - (83f)和(84a) - (84f)以及以下不同的微型电池问题
(89) (90) (91) (92) (93) (94)这些不同的分解和假设导致我们有良好的单元问题,当在单元边界上补充周期性条件时,一个额外的唯一性条件可以很容易地解决,以确定宏观尺度模型的系数。在这里,我们引入了一个更复杂的符号,强调了数量所依赖的尺度,并显示了预应力分解为局部和全局分量。尽管这增加了符号的复杂性,但与假设预应力完全依赖于微观尺度和宏观尺度时相比,所得到的模型实际上可以以更低的计算成本求解。实际上,我们发现预应力的分解导致宏观尺度和微观尺度问题之间的完全解耦,从而消除了本小节前面所讨论的问题。因为我们有这种解耦,然后我们解决六个弹性型单元问题(83a) - (83f),矢量问题(84a) - (84f),然后矢量问题(85a) - (85f)和(86a) - (86f)或(89)-(94)。
微观变化的预应力
如果我们假设预应力只依赖于微观尺度,那么我们可以得到宏观尺度模型(79a) - (79d);然而,我们可以注意到有效应力,
(95)包含作为项的预应力。这意味着,当我们在宏观尺度平衡方程中使用有效应力时,这些预应力项将消失,因为它们只依赖于微观尺度。也就是说,
(96)与以前一样,流体的细胞问题不涉及预应力,因此仍为(48)。对于实体单元部分,我们有问题(57a) - (57f)和(58a) - (58f)不受预应力影响;但是,(59a) - (59f)会受到影响。我们可以看到(59a) - (59f)我们有预应力。在单元问题中,我们将预应力张量的微尺度散度和预应力差作为单元问题的驱动力。由于这些预应力仅依赖于微观尺度,因此两个尺度完全解耦。然后,细胞问题是一般的渐近均质化类型,它只取决于微观尺度,因此可以用一种直接的方式解决。例如,对于线弹性复合材料[27],孔隙尺度渐近均匀化单元问题在[44]中得到了解决。[32]解决了线性孔隙弹性问题,研究了孔隙率和微尺度固体基质压缩性对孔隙弹性材料力学行为的影响。最近,在[34]中解决了多孔弹性复合材料的细胞问题,对多孔弹性复合材料的有效刚度进行了微观力学分析。预应力取决于微尺度的情况只适用于增材制造的金属材料,如不锈钢,这些材料通常具有大量的微尺度残余或预应力[48]。
宏观变化的预应力
最后,我们考虑了预应力和仅依赖于宏观尺度的情况。我们有相同的宏观模型(79a) - (79d)。同样,除了细胞问题(59a) - (59f)外,所有问题都保持不变。我们用下面的分解方法来写第一阶预应力
(97a) (97b)在这种情况下,我们看到弹性问题(54a) - (54f)可以写成如下,因为和没有依赖关系,
(98a) (98b) (98c) (98d) (98e) (98f)在我们为弹性问题(98a) - (98f)提出的分析中,我们还需要考虑这个分解(97a)和(97b)。我们可以使用(82a)和(82b),我们得到(57a) - (57f)和(58a) - (58f),它们现在是依赖的,因为我们做了假设(80),我们也得到了下面两个细胞问题
(99a) (99b) (99c) (99d) (99e) (99f)和
(100a) (100b) (100c) (100d) (100e) (100f)这个分解是(81a)和(81b)的特殊情况。这些不同的分解和假设导致我们有良好的单元问题,当补充了单元边界上的周期性条件,以及一个额外的唯一性条件时,可以很容易地解决,以确定宏观尺度模型的系数。预应力仅依赖宏观尺度的情况,可适用于预应力锚固节理岩体剪切损伤的本构模型[49]。
我们现在提出了一个解决完整宏观尺度模型(79a) - (79d)的方案。当预应力仅取决于微观尺度时,或者当预应力仅取决于宏观尺度时,如第4.1节所述,可以使用以下方案来求解预应力的建议分解。我们提供了一个清晰的分步指南,说明如何找到模型的有效系数,然后在解决宏观尺度模型(79a) - (79d)时如何使用这些系数。模型系数编码结构细节,如几何和弹性特性。在本指南中,我们包含了特定的参考文献,这些参考文献将帮助读者理解要进行的数值模拟类型,以找到系数并求解最终模型,如[32,34]。
我们假设了材料的全球尺度均匀性,并假设两个尺度通过第4.1节中讨论的情景之一完全解耦;然后,我们可以提出以下步骤来求解模型。流程如下:
第一步是在微观尺度上固定弹性基体和弹性亚相的原始材料性质。我们假设每个弹性相都是各向同性的。这意味着我们为矩阵和子相固定了两个参数。这是两个独立的弹性常数,如泊松比和杨氏模量(或者取决于可用的实验测量,lam
然后我们必须固定微尺度的几何形状,这意味着我们确定了单个周期电池的特定几何形状,包括每个相的体积分数。
下一步是找到宏观尺度模型系数。我们从固体(弹性)系数开始。我们解决弹性型单元问题(57a) - (57f), (58a) - (58f), (59a) - (59f),以获得宏尺度模型系数中出现的辅助张量,,,,和。要解决的电池问题在于组件
(101a) (101b) (101c) (101d) (101e) (101f)和
(102a) (102b) (102c) (102d) (102e) (102f)和
(103a) (103b) (103c) (103d) (103e) (103f)我们在哪里用过这个符号
(104a) (104b) (104c)(101a) - (101f)问题的解是通过固定一对指标求解六个弹性型单元问题得到的。当我们这样做的时候,我们可以看到我们有应变,所以对于每一对固定的指标k,我们有一个线性弹性问题。有关此过程的更多细节,请参见[32,34]。(102a) - (102f)和(103a) - (103f)是向量问题。这些法线的驱动力在矩阵和空穴之间或者在子相和空穴之间或者在矩阵和子相之间以及在前序预应力上的差异取决于你要解决的问题。法线编码空隙的几何形状,并用于计算解。我们注意到,这里我们提供的是最一般的单元问题,根据预应力的性质,使用4.1节中出现的单元问题的修改版本可能是合适的,有关部件中的所有单元问题,请参阅附录A。
为了保证解的唯一性,我们还需要一个附加条件。我们选择强制单元问题解决方案的单元平均值为零,即。
(105)我们也有与材料中流体流动有关的系数。我们有流体单元问题(48),通过求解得到宏观尺度系数中出现的张量和矢量。要解决的电池问题是组件
(106) (107) (108)由单元问题(,,,,,和)产生的辅助二级张量然后用于获得宏观尺度模型的系数。
必须规定宏观结构和几何形状。我们还设置了均匀化细胞的边界条件,并提供了宏观尺度固体位移和压力的初始条件。
最后,我们的宏观尺度模型就可以求解了。要了解更多细节,请考虑[33]
最后,我们希望将宏观尺度模型(79a) - (79d)与[40]中发现的电致伸缩复合材料的宏观尺度模型进行比较。在[40]的工作中,使用渐近均质化技术推导出一个宏观尺度模型,该模型捕获了线性弹性复合材料的行为,该复合材料的变形是由给定张量的散度驱动的,其中该张量与麦克斯韦应力张量一致。[40]的形式结果可以与我们在没有流体相的情况下的结果进行比较。由于在[40]中没有流体的贡献,那么我们可以首先考虑将(79a) - (79d)减小到没有流体的情况。我们将只保留平衡方程(79b),并将修改本构律(79c)。也就是说,我们的简化模型由
(109a) (109b)为了进行更精确的比较,我们可以使用3.3节中介绍的符号(34)将本构律重写为
(110)然后我们可以看到平衡方程(79b)和本构律(110)正是[40]中的式(60)、式(61a)和式(61b)。我们有
(111)其中,我们称之为预应力的张量和与[40]用作广义麦克斯韦应力张量的张量相同。
我们还可以将这里得到的细胞问题与[40]中的进行比较。由于公式[40]中不涉及流体,因此我们再次只需要固体弹性单元问题。这意味着我们只需要(57a) - (57f)和(59a) - (59f)修改为无流体的情况。这就意味着这些细胞问题将会变得
(112) (113) (114) (115)和
(116) (117) (118) (119)使用我们上面所做的符号识别,我们可以看到这些正是在[40]中发现的细胞问题(44a-44d)和(45a-45d)。
在整个工作过程中,我们在准静态状态下推导了一个新的偏微分方程系统,该系统描述了受预应力作用的多孔弹性复合材料的有效力学行为。我们研究的材料具有微观结构,包括多孔弹性基体和亚相,孔隙中流动着不可压缩的牛顿流体。弹性矩阵和各个子相假定为线弹性,但都是预应力的。具有这种微观结构的材料在现实世界中有许多应用,包括生物组织的建模,如动脉壁。另一个可以通过使用本手稿中开发的多尺度方法来研究的生物学问题是病灶粘连,例如,通过扩展[50,51]中提出的分析,其中考虑了非弹性过程。
为了推导出这种类型的微观结构的新模型,我们创建了一个流体-结构相互作用(FSI)问题,该问题适当地描述了几何结构的每个组成部分。通过在结构中存在的三个不同的接口上应用一些接口条件来关闭问题。我们在基质与流体界面以及子相与流体界面上应用了引力和速度的连续性。我们还应用了不同弹性子相与基体之间的牵引力和位移的连续性。我们知道,在微观尺度(所有个体相都清晰可见)和宏观尺度(材料的平均长度)之间存在明显的长度尺度分离,因此我们能够应用渐近均质化技术来推导控制材料行为的新模型。新获得的控制方程的系数编码了精确的几何和材料性能的微观结构细节。我们能够通过解决由于使用渐近均匀化技术而产生的周期单元问题来计算模型系数。然后,我们研究了不同的预应力选择,这将影响整体宏观模型和决定模型系数的单元问题。我们提供了一个解决宏观模型的方案,并在附录中说明了组件中可能出现的细胞问题。最后,我们假设模型不存在流体相,并在电致伸缩弹性复合材料上恢复[40]模型。
本文获得的新模型是对[28]的重要扩展,可以认为是对具有详细微观结构的孔隙弹性材料(如生物组织)现有模型的有益改进。这项工作的关键新颖之处在于考虑了在每个弹性阶段存在的预应力的影响。通过考虑预应力,我们推导出[28]模型,其中包含编码这些应力的附加项和系数。我们发现预应力渐近展开的首阶项出现在材料的宏观本构律中,是新单元问题(59a) - (59f)的驱动力。这个单元问题,连同(57a) - (57f)和(58a) - (58f),可以求解出编码微观结构的几何和刚度细节以及张量的系数,这些系数出现在宏观尺度模型的本构律和质量守恒方程中,并解释微观结构中不同部位的预应力变化。由于这些细胞问题,我们能够直接解释宏观控制方程中的微观复杂性。
我们导出的模型受到一些限制,如果期望的应用程序需要,可以很容易地进行修改。我们制定了一个准静态和线性化的宏观模型。这意味着我们没有考虑线性化惯性。然而,很有可能放宽这一假设,这将在我们的宏观尺度模型有效平衡方程(79b)中产生额外的项。这些惯性项的加入对肺部建模的应用很有用,其中声学特性可以用来帮助肺部疾病的诊断[52,53]。
我们还在线性弹性环境下制定了这个模型。理论模型可以扩展到非线性弹性,是[31]的特殊扩展。通过扩展到非线性设置,我们创造了进行数值模拟的复杂性。这种复杂性的出现是因为系统中的两个长度尺度保持耦合,导致计算负载增加。有一些新兴技术可以潜在地解决这些模型,同时在计算上不太昂贵,例如使用人工神经网络[46,54]。
该理论也适用于粘弹性的研究。最近的工作[55]考虑了由几个弹性相和一个流体相组成的底层微观结构,当通过渐近均匀化放大时,给出了粘弹性复合材料的kelvin - voigt型模型。这是可能的延伸,假设固体相确实是预应力的。分数粘弹性最近被用于分析描述各种异质生物材料行为的实验数据。在[56]中,考虑了具有粘弹性本构响应的复合材料的有效性能,其中每个组分都由分数粘弹性模型描述。这可以进一步发展,包括在复合材料的每个组成部分的预应力。
为了进一步推进模型,有必要使用特定的微观结构和由现实世界数据选择的参数来获得模型的解。这些数据可能与各种各样的生物例子有关,包括动脉壁和心肌。在文献中,标准Biot孔隙弹性的宏观尺度模型由[33]求解,孔隙弹性的微尺度单元问题由[32]求解,孔隙弹性复合材料的微尺度单元问题由[34]求解。
发表评论
暂时没有评论,来抢沙发吧~