随机数在计算机科学的许多领域都非常重要。仅使用基本的算术运算生成高质量的随机数是具有挑战性的,特别是对于硬件功能有限的设备,例如物联网(IoT)设备。本文提出了一种新的基于抽象自动机组合的伪随机数生成器——简单链自动机随机数生成器(SCARNG)。该算法的主要优点是结构简单,可以很容易地实现非常低计算能力的物联网系统,fpga或GPU硬件。生成的随机数展示了有希望的统计行为,并满足NIST统计套件的要求,突出了SCARNG在实际应用中的潜力。
随机数生成在计算机科学的许多领域都非常重要,包括蒙特卡罗模拟[1]、密码学和其他计算机应用。伪随机数发生器(pseudorandom number generators, PRNG)的研究受到了研究者的极大关注,数学的各个领域都被用来产生随机数,如数论[2]或混沌理论[3]。利用自动机理论生成随机数在文献中并不新鲜。早在1986年,S. Wolfram就提出了一种使用元胞自动机生成随机数的方法[4]。1989年,Hortensius等人利用一维元胞自动机提出了VLSI系统的随机数生成[5]。从那时起,文献中发表了许多基于各种类型的元胞自动机的文章(例如,参见[6,7,8,9,10])。元胞自动机的简单构造使其成为生成随机数或开发新密码系统的有吸引力的选择;然而,这种简单性也使它们容易受到特定类型的攻击[11,12]。因此,基于不同于元胞自动机的自动机理论原理,探索创建新的伪随机数生成器和加密方案是合理的。
本文的目的有两个:开发一个非常简单的自动机,成功通过已知的统计测试,并创建一个结构非常简单的PRNG,适用于嵌入式设备和物联网(IoT)应用。物联网是一个无处不在的、无处不在的物理对象网络,这些物理对象嵌入了传感器、软件和其他技术,使它们能够通过互联网或其他通信网络与其他设备和系统连接和交换数据[13]。这些相互连接的设备可以相互通信,收集数据,并自主执行各种任务;因此,在复杂的物联网环境中,确保每个设备的保护至关重要。与传统的计算机系统相比,在这些环境中使用的物联网设备通常是低成本的RFID标签、传感器、缺乏足够处理能力和存储能力的非接触式智能卡。因此,标准加密原语可能不适合物联网端点,并且执行经典网络攻击通常比在典型计算机系统上更容易,使其成为恶意用户的潜在目标[14]。轻量级加密通常用于解决受约束环境的安全问题;然而,物联网设备的多样性在物联网系统的加密原语设计中提出了重大挑战。
在本文中,作者继续他们基于抽象有限自动机组合的加密工具的联合研究[15,16]。2021年,作者提出了一种基于自动机组合的全周期长度计数器的PRNG[17]。所提出的构造的有希望的统计行为激发了我们探索开发基于自动机组合的更简单生成器的潜力。PRNG背后的主要思想是随机数作为自动机的给定Gluskov积的状态转换而生成,其中该Gluskov积的状态被认为是给定长度m的二进制字符串。更准确地说,对于所考虑的Gluskov积的适当固定状态和固定输入字母x,生成的伪随机数为,其中表示复合自动机的转换函数,对于每个。结果表明,该生成器产生了高质量的数字,并通过了众所周知的统计测试,但该方法的一个显著缺点是所考虑的自动机组成的复杂性。在本文中,我们引入了一种更简单、更紧凑的PRNG,我们称之为简单链自动机随机数生成器(SCARNG)。本文提出的算法的主要优点是其结构简单,可以在fpga, gpu和物联网设备上以最小的计算能力轻松实现。本文提出的算法已经成功通过了美国国家标准技术研究院(NIST)的统计检验[18]。此外,引入的链式自动机的独特性质可以开辟新的研究方向。
本文介绍了无缝理解所需的所有概念。然而,本文不包括自动机理论的基本原理及其介绍。对于基本的符号和对主题的进一步了解,我们建议读者阅读由D?m?si和Nehaniv[19]撰写的SIAM关于自动机网络代数理论的专著。
像往常一样,让我们用一个有限的非空的符号集合来表示,我们称之为字母表。对于任意集合,让我们表示上的自由幺一元,它的意思是字母表上所有字符串的集合。设为空字的单位元素。然后,对于每一个;此外,对于每一对,无论何时对于一些,和。另外,对于每一个,每一个正整数,设。
所谓自动机,我们指的是没有输出的确定性有限自动机。更准确地说,自动机是由非空有限状态集A、非空有限输入集和过渡函数组成的代数结构。自动机的转换矩阵由一个矩阵表示,其中行与每个输入相关联,列与每个状态相关联。对于用input表示的任意行和用state表示的任意列,矩阵条目包含状态。如果转移矩阵的所有行都是状态集的置换,那么我们就说置换自动机。
我们将以通常的扩展形式使用自动机的过渡函数的概念。给定一个自动机,它的扩展转移函数是映射,其中表示上的自由单阵,并通过以下递归定义扩展到:对于每个状态,对于每个三元组,。n阶拉丁方阵是一个矩阵(有n行n列),其中每个单元格由n个元素集合中的一个元素填充。每个元素在矩阵的每行和每列中只出现一次。在本文中,我们将考虑一种特殊的自动机组合,称为键自动机,其状态转移表形成拉丁方。通过这些特性,所考虑的伪随机数生成器对统计攻击具有很强的免疫力。在介绍发电机的精确设计之前,我们将首先介绍了解SCARNG结构所需的几个基本概念。
设为自动机其中取一个有限非空集和反馈函数对于每个a Glu?kov-type自动机对反馈函数的积被定义为具有状态集输入集转移函数的自动机为所有,特别地,如果,那么我们说这是一个Glu?kov-type幂。
下面是最简单的Glu?kov-type幂函数之一。设一个自动机,其状态集与输入信号集一致。给定正整数n,定义自动机,对于每一对,,其中下一状态向量的第一个分量是自动机状态转移链的结果,在输入信号分量的作用下,该链的最后一个成员从当前状态进入下一个状态,在输入信号的作用下,链上的每一个成员都从它的状态进入到下一个状态,这与所考虑的自动机链上的成员的状态转移的结果是一致的。对于每一步,我们重复这个过程,使初始状态改变为。在公式中,让。从现在开始,将上述构造的自动机称为链动力。链动力状态转换示意图如图1所示。
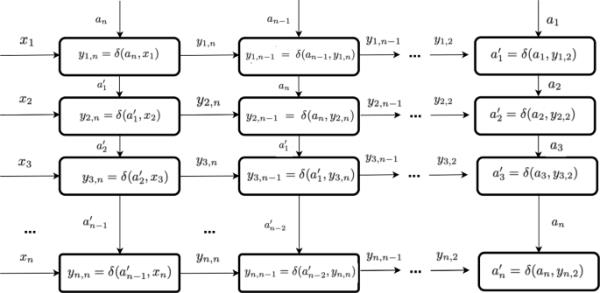
链式动力状态转换
假设这是一个排列自动机。那么,每一个链幂也是一个置换自动机。
假设这是一个排列自动机。那么,根据定义,其转移矩阵的所有行都是状态集的置换。因此,这些行都不包含重复。因此,对于任何状态和输入暗示。给定一个正整数n,设它是的链幂,并假设它不是置换自动机。然后,它有不同的状态和输入符号对于某些假设这是最大的指标。然后,根据定义,还有。回想一下,这是一个排列自动机。显然,这与假设相矛盾。因此,应该是一个排列自动机。这就完成了证明。
假设一个自动机的转移矩阵形成一个拉丁平方。那么每一个链的幂也有这个性质。
考虑一个自动机,并假设它的转移矩阵形成一个拉丁平方。设它对某正整数n的链幂。根据命题1,是一个置换自动机。因此,可以证明,对于每一个状态和不同的输入信号对,放和。设为最小索引。那么,根据定义,要么,要么。若则与。的转移矩阵形成一个拉丁平方。显然,利用这个变换矩阵的列也是的排列,我们有。电感。因此,我们准备好了。否则,使用。因为的跃迁矩阵的列是的置换,我们有,归纳地,,。的变换矩阵的列是的置换。然后,我们收到。因此,正如我们所说的。证据是完整的。
设一个自动机,它的转移矩阵形成一个拉丁方阵。给定一个正整数n,考虑的链式幂。从现在开始,我们说这是一个关键的自动机。
使用整数计数器作为生成器的唯一内部状态是开发伪随机数生成器的一种众所周知的方法,称为基于计数器的PRNG(参见示例[20])。
状态转移函数是有限状态集大小n的一个模的增量,复杂度来自于从状态到随机样本的映射。形式上,基于计数器的伪随机数生成器(CBPRNG)是一个结构,其中K为键空间;,其中J是一个正整数,称为输出多重性;S是状态空间;U为输出空间;为状态转移函数,;是输出函数。
在离散的时间尺度上工作。它从一个固定的状态开始,称为初始状态和一个固定的键。那么,对于每一步,生成的随机数序列为,,其中和。在这种情况下,这个向量,被称为初始状态的输出向量。
给定a,我们说它的状态转移函数有一个完整的周期,如果对于每个,,其中,根据定义,表示s的基数,并且,如果对于任何键和初始状态,在返回到初始状态的输出向量之前遍历每个输出向量,则我们说a有一个完整的周期或完整的周期。
为简单起见,假设S是一组固定长度相同的二进制字符串。我们说,如果是最小正整数n,它的周期是平凡的。
A有一个满循环当且仅当它的状态转换函数有一个满循环,并且对于每一个键,函数都是双射的。
如果集合是单态的(即),那么我们将把g写成这种形式,然后,我们说它有一个简单的输出多重性。在这种情况下,我们也会写成这种形式。为了简单起见,本文中我们认为cbprng具有简单的输出多重性。脚注2
给定一个具有简单输出多重性的输出函数,假设。我们说输出函数是输出函数的二次循环。一般来说,我们说这是一个-乘以一轮的if对于每一个这样的是-乘以一轮的。最后,单轮的是函数本身。
对于cbprng,我们应该让g是复杂的,f是一个简单的计数器,其中p是以位和为单位的状态大小[20]。应用这一构造思想,本文考虑cbprng,其中f为计数器,g由抽象有限自动机的组合定义。
给定一个非空集合,put for every和with。考虑一对非空集合、一个正整数和函数。假设对每一对都成立。然后,我们说g代表一轮中的f。此外,如果存在这样一个条件,对于每一对,它都成立,那么我们说f表示g在t轮中。
给定一个正整数,每个键自动机转换函数表示一个基于计数器的伪随机数生成器的输出函数(具有简单的输出多重性)。
为了证明我们的观点,我们给出了一个适当的基于计数器的PRNG (CBPRNG)的构造,它具有这个性质。首先,考虑一个计数器,它实现状态函数为,其中m是一个足够大的正整数(最好),n是一个固定长度的二进制数(最好是128位长度)。
因此,状态空间为。
的状态集S的元素可以看作是固定长度的二进制字符串。我们假设状态空间S重合于,其中为输入集,对于一个合适的正整数。并且,我们还假设输出集U和键空间与K重合。
另外,假设的输出函数为,对于每一个都是固定的。显然,过渡函数代表输出函数g,这就完成了证明。
根据命题3和定理4,我们可以推出如下内容:
设为一个基于计数器的伪随机数生成器,具有简单的输出多重性(即),并假设给定密钥自动机的过渡函数表示的输出函数。如果它是单轮的,那么它有一个完整的周期。
回想一下,根据定义,对于每个键自动机,其基本自动机的转移矩阵形成一个拉丁平方。因此,根据定理2,所有键自动机的转移矩阵都具有这个性质。因此,它们的转移矩阵的所有行和所有列都是其状态集的置换。
当然,因为状态转换f(具有简单的输出多重性)是一个简单的计数器,其中p是以位为单位的状态大小,f有一个完整的周期。而且,根据定理2,键自动机是一个置换自动机;因此,对于每一个输入符号,与都是到自身上的一个双射映射。因为,。显然,这个函数也是双射的,其中g表示的输出函数。根据命题3,这意味着(具有简单的输出多重性)有一个完整的周期。
考虑一个键自动机,它的过渡函数表示给定的t轮的输出函数g。那么g的形式是。那么,带for的函数一般不是双射的。因此,如果,则表示的输出函数不一定有一个完整的周期。
在本节中,我们给出了一个例子,然后研究了我们的CBPRNG的安全性,我们称之为简单链自动机随机数生成器(SCARNG)。该生成器的主要优点是它的简单性,并且可以很容易地在物联网设备上实现。所提出的发生器的结构非常简单,如图2所示。
所提出的自动机只使用基本的算术运算。算法1给出了SCARNG的详细伪代码。

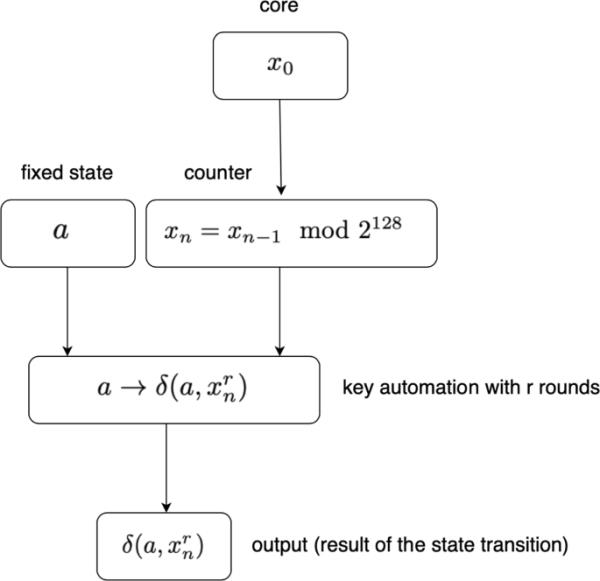
带有r轮的简单链自动机随机数生成器(SCARNG)
过程参数是随机块数(SIZE)、键自动机的输入字(input)、基本自动机的转移矩阵(AUT)和键自动机的初始(种子)状态(ISTATE)。每个生成的随机块由128个随机字符串组成,每个随机字符串长度为128位。因此,生成的随机块的大小为2048字节。关键自动机是一个自动机的圆分量时间幂,该自动机是基本自动机的16分量链幂,该基本自动机具有一个形成拉丁方的型转移矩阵。因此,每个状态和输入符号都可以用一个8位二进制字符串表示。我们将使用一个型辅助矩阵P,其中它的第一行由向量组成,所有其他的都是前一行的循环排列。我们将考虑CBPRNG输出函数的轮数。由16个分量组成的向量INPUT表示键自动机的单个输入符号。
在本节中,我们将展示一个简单的示例。考虑以下自动机的过渡表脚注3:
0 |
1 |
2 |
3 |
|
|---|---|---|---|---|
0 |
1 |
2 |
3 |
0 |
1 |
3 |
0 |
1 |
2 |
2 |
2 |
3 |
0 |
1 |
3 |
0 |
1 |
2 |
3 |
为简单起见,假设,即密钥自动机由三因子链幂组成,且设轮数为3。假设计数器的后续状态,即键自动机的后续输入信号,通过应用公式或在四进制中确定,从而生成的伪随机数为三位四进数。设核心状态,即计数器的初始状态为203。因此,在这种情况下(采用四进制进行计算),即键自动机的第一个输入信号在四进制中。设123为密钥自动机的固定状态(由密钥自动机所表示的链功率的第一、第二和第三分量自动机组成)。在这种情况下,使用,,,,。
因此,在第二轮中,和之前一样,我们有。因此,我们得到
,,。
因此,在第三轮,和之前一样,我们有。因此,我们通过以下方式得到第一个伪随机数。
,,。
那么,第一个伪随机数将是三位四进制数101。
然后,我们要么完成我们的过程,要么生成第二个伪随机数。当产生第二个伪随机数时,重复该过程,使密钥自动机的状态和输入信号(以四进制给出)相同,等等。
为了测量生成器的实际运行时间和统计特性,我们在c++中实现了SCARNG算法。测试环境是配备第7代Kaby Lake 2.9 GHz英特尔酷睿i7处理器(7820HQ)的2017年MacBook Pro,使用16gb RAM。我们生成了1gb的随机数据,并应用了NIST统计随机性检验。
美国国家标准与技术研究所(NIST)发布了一个统计软件包,其中包含15个统计测试,用于测试由基于硬件或软件的加密随机或伪随机数生成器产生的任意长二进制序列的随机性[18]。对于每个统计检验,都会产生一组p值。给定显著性水平,如果p值小于或等于,则检验表明观察到的数据与我们的零假设(即“随机性假设”)不一致,因此我们拒绝它。
我们使用显著性水平为,因为它是密码学和PRNG测试领域中此类问题的标准值。如果显著性水平设置为0.01,则意味着可以期望在零假设下拒绝100个序列中的一个序列。因此,p值大于0.01表示序列是随机的,而p值小于或等于0.01表示序列是非随机的。
PRNG最重要的特征之一是与真实随机源的不可区分性。这意味着应用于PRNG输出的任何统计测试都不应该揭示它与真正随机源之间的任何计算差异。为了测试SCARNG的质量,使用与AES候选数据相同的参数进行了NIST SP-800-22 SP统计测试,以获得最可靠和可比较的结果。序列长度、样本量、显著性水平等参数均固定。也就是说,这些参数分别设置为位,300个二进制序列,和。其他输入参数如表1所示。
仅应用3轮,就发现SCARNG算法成功地满足了NIST统计测试套件概述的所有要求。事实证明,NIST统计测试套件无法将算法的输出(当使用ROUND=3时)与真正的随机源区分开来。在没有精确并行化的情况下,生成1gb随机数据的算法运行时间为27s。SCARNG评估的确切p值如表2所示。我们还检验了NIST中包含的统计检验获得的p值分布的均匀性。p值的均匀性没有提供有关应用PRNG的额外信息。我们还表明,超过0.01水平的二值序列的比例位于所需的置信区间内。为了进一步了解测试方法,我们参考了NIST文档[18]。
发表评论
暂时没有评论,来抢沙发吧~